Vanuit mijn werk als GIS specialist ben ik gewend aan het visualiseren van gegevens op de kaart in verschillende ruimtelijke schalen. In Nederland kun je met de Basisregistratie Adressen en Gebouwen (BAG) en de Basisregistratie Grootschalige Topografie (BGT) inzoomen tot de schaal van gebouwen en onze directe leefomgeving. Soms is de buurten schaal nodig en dan gebruik ik de buurtgrenzen van het CBS. En toen ik me met planeetonderzoek bezig hield was ik geïnteresseerd in de continentale schaal en de schaal van de hele planeet. Één ding dat ik toen al heel interessant vond was de vraag hoe deze schalen zich verhouden. Denk bijvoorbeeld aan fractals, patronen die zich in verschillende schalen herhalen (Figuur 1).

Figuur 1. Een varenblad is een voorbeeld van een fractal: de verschillende blad delen hebben hetzelfde patroon als het blad zelf. Dit plaatje is het resultaat van python code.
Zodoende was het niet vreemd dat ik meteen gepakt werd door het boek Schaal van Geoffrey West (2017). Het boek geeft een uitgebreide beschrijving hoe de natuur bepaalde wetmatigheden lijkt te volgen rond schaal. Zo stelt de Wet van Kleiber dat er een verband is tussen de massa en stofwisseling van dieren. Het energieverbruik van dieren blijkt namelijk evenredig met de massa verheven tot de macht 0.75. En als je dit op een logaritmische schaal weergeeft krijg je een rechte lijn (Figuur 2).

Figuur 2. De stofwisselingssnelheid (metabolic rate) van verschillende dieren versus hun massa. Voor meer informatie zie deze en deze links.
Dezelfde soort wetmatigheden beschrijft West in zijn boek ook binnen de door mensen gecreëerde wereld: bij steden, bedrijven en sociale netwerken. Ik ga hier nu niet in op zijn analyses van bedrijven en sociale netwerken, vooral zijn voorbeelden van onderzoek naar steden vind ik vanwege het ruimtelijk aspect erg interessant. Bij het lezen van het boek had ik ook steeds de vraag in mijn achterhoofd of deze wetmatigheden wellicht kunnen helpen bij de energietransitie-opgave. Daar kom ik straks op terug.
Steden bestaan uit verschillende infrastructuur netwerken, zoals wegen, elektriciteitskabels, waterleidingen en warmtenet buizen. Deze lijken qua patroon op biologische netwerken zoals het bloedvatenstelsel in ons lichaam. Of in de woorden van West, “de manier waarop in infrastructurele netwerken de stroming systematisch afneemt vanaf de centrale bevoorradings eenheden – zoals energiecentrales en waterleidingbedrijven – via de kabels en leidingen naar afzonderlijke huizen, lijkt in veel opzichten op de manier waarop de bloedstroom in het bloedvatenstelsel afneemt in min of meer regelmatige geometrische verhoudingen vanaf het hart via de aorta naar de haarvaten die de cellen bedienen.”
Er lijkt namelijk een verband te bestaan tussen de totale lengte van infrastructuur binnen een stad en de grootte van de stad, uitgedrukt in het aantal inwoners. Een voorbeeld van een lijnen netwerk zoals wegen vond ik niet in het boek, wel het aantal benzinestations (voorbeeld van een netwerk node) uitgezet tegen het aantal inwoners (Figuur 3). Het aantal benzinestations blijkt evenredig met het aantal inwoners verheven tot ongeveer de macht 0.85. De take home message hier is dus dat een twee keer zo grote stad niet twee keer zoveel benzinestations nodig heeft. Oftewel, “een stad met tien miljoen inwoners heeft 15 procent minder van dezelfde infrastructuur nodig dan twee steden van elk vijf miljoen, wat leidt tot een aanzienlijke besparing in materiaal en energiegebruik”, aldus West.
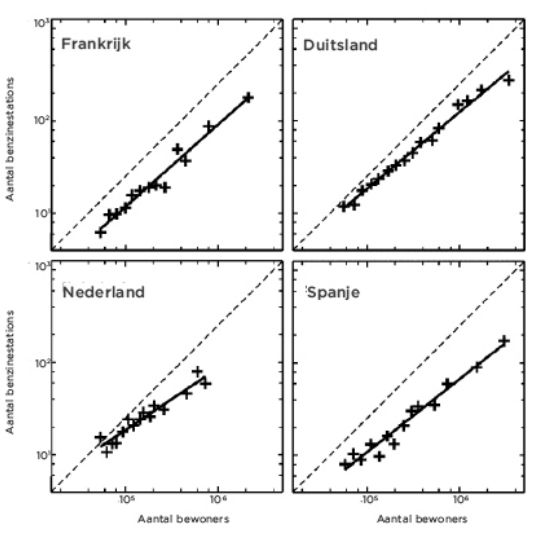
Figuur 3: Figuur 33 uit Schaal. Voor vier landen is het aantal benzinestations en het aantal inwoners van steden tegen elkaar uitgezet op een logaritmische schaal. De stippellijn geeft een lineaire schaal aan.
Het is niet super moeilijk om het Nederlandse diagram van Figuur 3 te verifiëren. De TOP10NL dataset bevat hiervoor namelijk precies alle informatie: de woonkernen inclusief het aantal inwoners en de gebouw locaties met o.a. tankstations. Vervolgens vroeg ik mij af, wat definieert nou een stad? Het meest logisch leek mij het handmatig samenvoegen van elkaar rakende woonkern grenzen (Utrecht en Nieuwegein vormen bijvoorbeeld een praktisch aaneengeschakeld stedelijk gebied). Vervolgens heb ik in QGIS het aantal inwoners van deze aan elkaar liggende woonkernen opgeteld en het aantal benzinestations berekend. Voor de grootste 40 stedelijke gebieden (Figuur 4) heb ik eenzelfde diagram als het figuur uit Schaal gemaakt (Figuur 5). De automatische trendline formule berekening komt uit op 0.83, dichtbij de 0.85 uit Schaal.
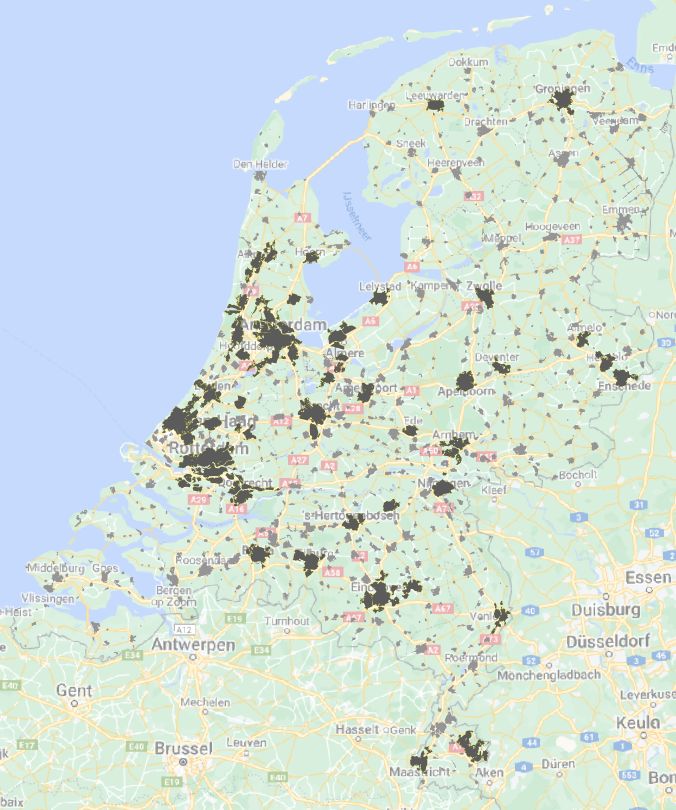
Figuur 4. De grootste 40 stedelijke gebieden (donker grijs) samen met alle andere woonkernen (lichtgrijs) uit de TOP10NL.
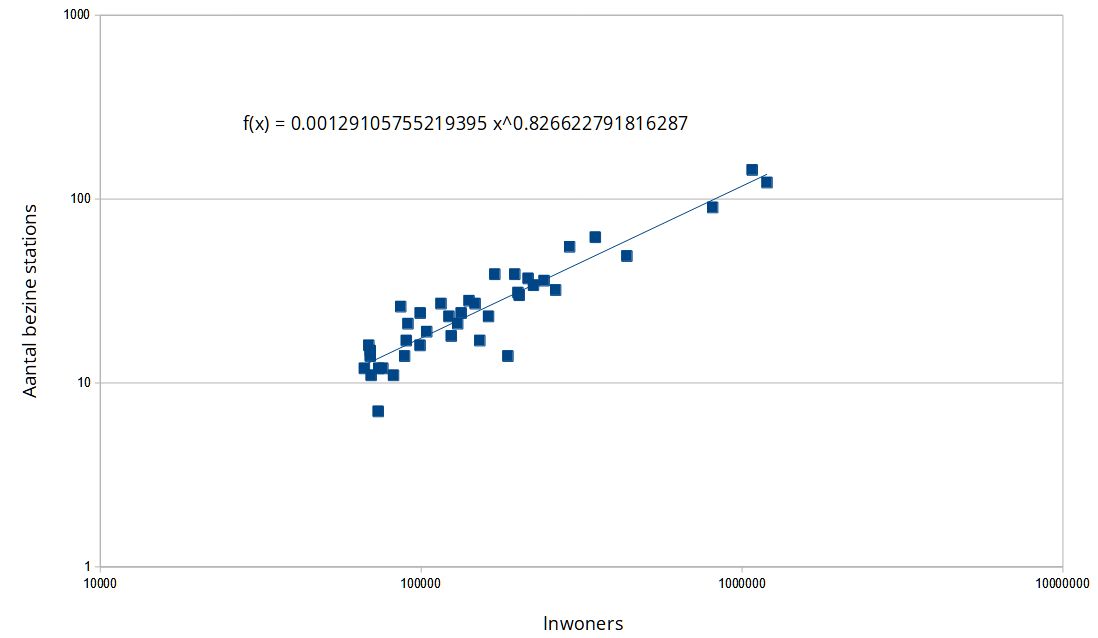
Figuur 5. Het aantal benzinestations uitgezet op een logaritmische schaal tegen het aantal inwoners van de 40 grootste stedelijke gebieden (Figuur 4).
Nu is de vraag, wat betekent dit allemaal? Kun je hier iets mee binnen de energietransitie-opgave? Hebben we misschien minder nodig dan we vanuit onze standaard lineaire logica zouden denken? En hoe zit het bijvoorbeeld met Utrecht en Nieuwegein? Zou een hechtere samenwerking plus het gebied als één metropoolgebied zien efficiëntere infrastructuur tot gevolg kunnen hebben (gehad)? Gebeurd dit al in de vorm van de (RES regio) U16? Als we het totale metropoolgebied van Utrecht als één stad zouden zien om van daar uit de infrastructuur te (her)ontwerpen, levert dit dan concrete besparingen op? Ik ben benieuwd of dit al eens onderzocht is.
Daar we in Nederland veel open geodata hebben kan naast benzinestation locaties nog meer infrastructuur op deze manier onderzocht worden zoals wegen en elektriciteitsnetwerken. Het lijkt me interessant om hier nog eens verder in te duiken.
Als laatste wilde ik nog noemen dat bij restaurants precies het omgekeerde lijkt te gebeuren dan bij benzinestations: een stad met twee keer zoveel inwoners heeft meer dan twee keer zoveel restaurants. Hier gaat volgens West wat anders spelen, sociaal gedrag van mensen, een grote stad is levendiger dan een kleine stad. Voor iedereen die daar meer over wilt lezen raad ik het boek Schaal van harte aan!